概要
波の性質のひとつに、重ね合わせの原理がありますね。
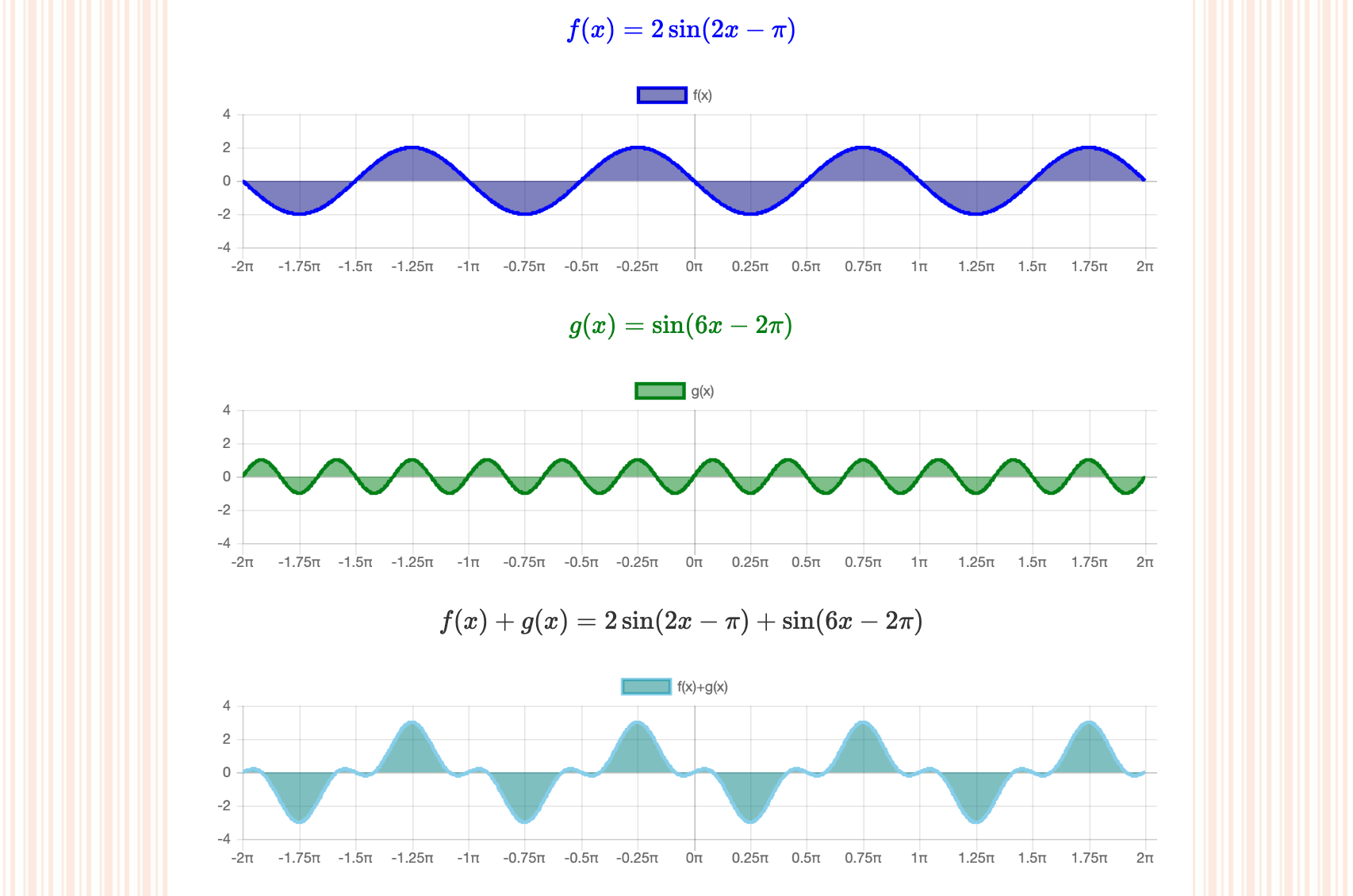
原理の説明はさておき、ここでは2つの波が重なった瞬間の形を見てみましょう。
重ね合わせる波
重ね合わせる波は、2つの正弦波 \(f(x),g(x)\) とします。
\begin{eqnarray}
f(x) = c_1 \sin(mx-a) \\
g(x) = c_2 \sin(nx-b)
\end{eqnarray}
好きなパラメータで試してみよう
説明することがないので、早速試してみましょう。
上式のパラメータ \(a,b,c_1,c_2,m,n\) を色々と変えて試してみましょう。
整数でなくても大丈夫です。
下記の条件を満たすように入力し、「表示」ボタンを押してください。
\(a,b\) は、それぞれ [入力値 × \(\pi\)] となります。
- \(-2\pi \leq a \leq 2\pi,-2\pi \leq b \leq 2\pi\)
- \(-2 \leq c_1 \leq 2,-2 \leq c_2 \leq 2\)
- \(-100 \leq m \leq 100,-100 \leq n \leq 100\)
\begin{eqnarray}
f(x) = c_1 \sin(mx-a) \\
g(x) = c_2 \sin(nx-b)
\end{eqnarray}
\(a=\) \(\pi\), \(b=\) \(\pi\)
\(c_1=\) , \(c_2=\)
\(m=\) , \(n=\)
———- 表示ここから ———-
———- 表示ここまで ———-