三角関数の内積と直交性

概要

フーリエ級数展開を理解する上で欠かせない、三角関数の直交性をみてみましょう。

関数の内積

ここでは、2つの関数 \(f(x),g(x)\)の区間\([a,b]\)の内積を次のように考えます。

\begin{eqnarray}
\langle f(x),g(x) \rangle = \int_{a}^{b} f(x)g(x)dx
\end{eqnarray}

積分区間が\([-\infty,\infty]\)になっている式も見たことありますが、ここではある区間\([a,b]\)にしか注目しません。あと、左辺に区間の記述が入っていないけど気にしない！

丁寧な説明を知りたい方は、次のページなどを読むと良さそう。関数の内積の捉え方を、ベクトルの内積の拡張として説明しています。

三角関数の内積

この記事では三角関数(sin,cos)にしか関心がありません。
積の順序は関係ないので、次の３種類の内積を考えることにします。

\begin{eqnarray}
\langle \sin(mx),\sin(nx) \rangle = \int_{a}^{b} \sin(mx) \sin(nx) dx \\
\langle \cos(mx),\cos(nx) \rangle = \int_{a}^{b} \cos(mx) \cos(nx) dx \\
\langle \sin(mx),\cos(nx) \rangle = \int_{a}^{b} \sin(mx) \cos(nx) dx \\
\end{eqnarray}

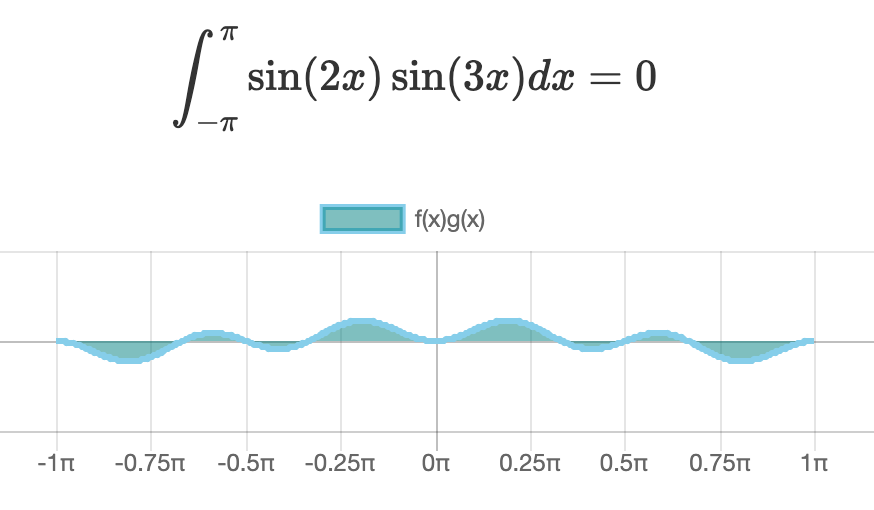
試しに、区間を\([-\pi,\pi],m=2,n=3\) として1つずつ見ていきます。それぞれの関数の積分と併せて見てみましょう。

sin同士の内積

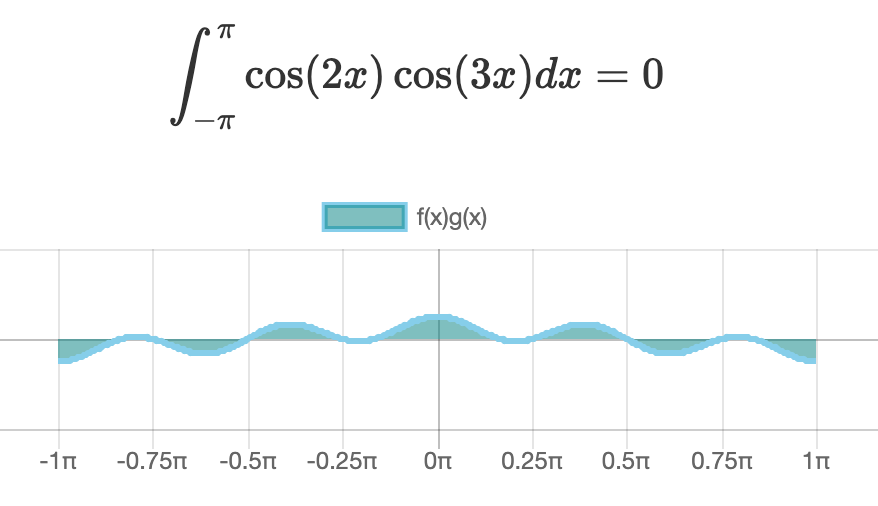
cos同士の内積

sinとcosの内積

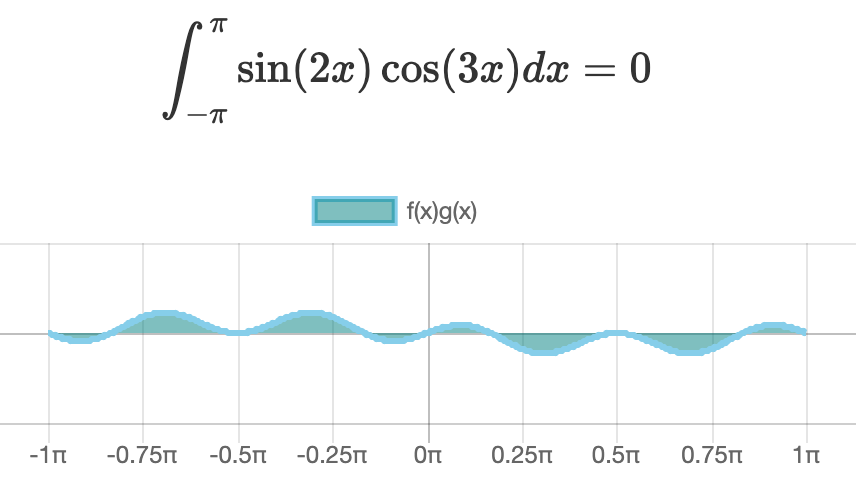
グラフを見ると、いずれの内積もプラス(x軸の上側)の面積とマイナス(x軸の下側)の面積が相殺して \(0\) になっている様子がわかりますね。

関数の直交性

上記の例のように、内積が \(0\) になる2つの関数 \(f(x),g(x)\) は、区間 \([a,b]\) で直交していると言います。もともと２つの直交したベクトルの内積が \(0\) であることから、関数にも直交という表現が拡張されたっぽいですね。

好きなパラメータで試してみよう

さて、よく知られている直交性については確認できましたので、ここからは好きなパラメータで内積を調べてみましょう。
上述の例では三角関数の周期に合わせて区間の長さを \(2\pi\) にしていました。また、三角関数の振幅は \(1\) にしていました。
これらのパラメータをいろいろと変更して内積を計算し、直交する条件を確認しましょう。