概要
ある関数を積分する様子を図でイメージします。
説明
まず、積分の定義は次のようになっています。
\begin{align}
\int_{a}^{b} f(x)dx = \lim_{n \to \infty} \sum_{k=1}^n f(x_k) \Delta ・・・(式1)
\end{align}
右辺の意味をわかりやすくするために、次のような数直線を考えます。
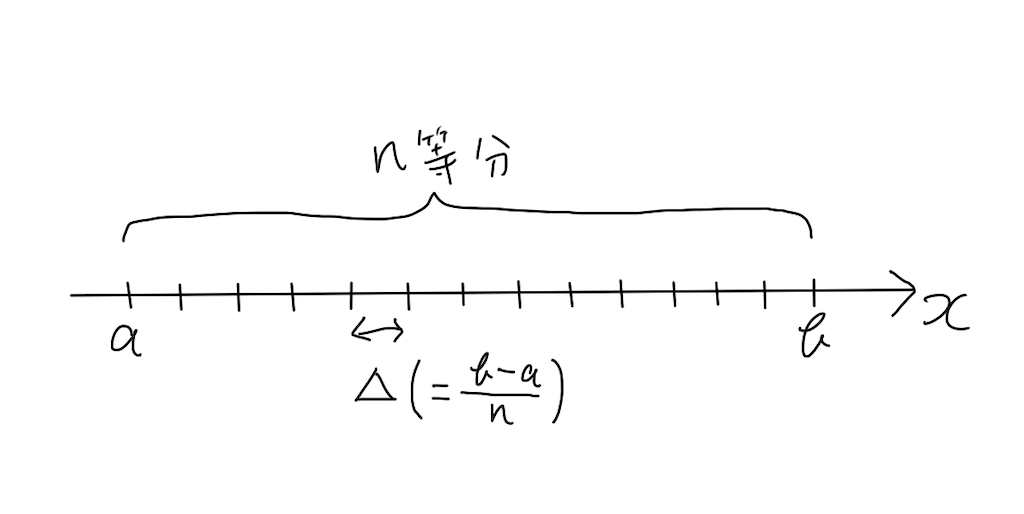
積分する範囲を \(n\) 等分し、1区間の幅を\( \Delta(=\frac{b-a}{n}) \)とします。
このとき、(式1)の右辺の和は、\(n=10\) のとき、
\begin{align}
\sum_{k=1}^{10} f(x_k)\Delta = f(x_1)\Delta + f(x_2)\Delta + ・・・ + f(x_{10})\Delta ・・・(式2)
\end{align}
となり、下図の長方形の面積の和になります。
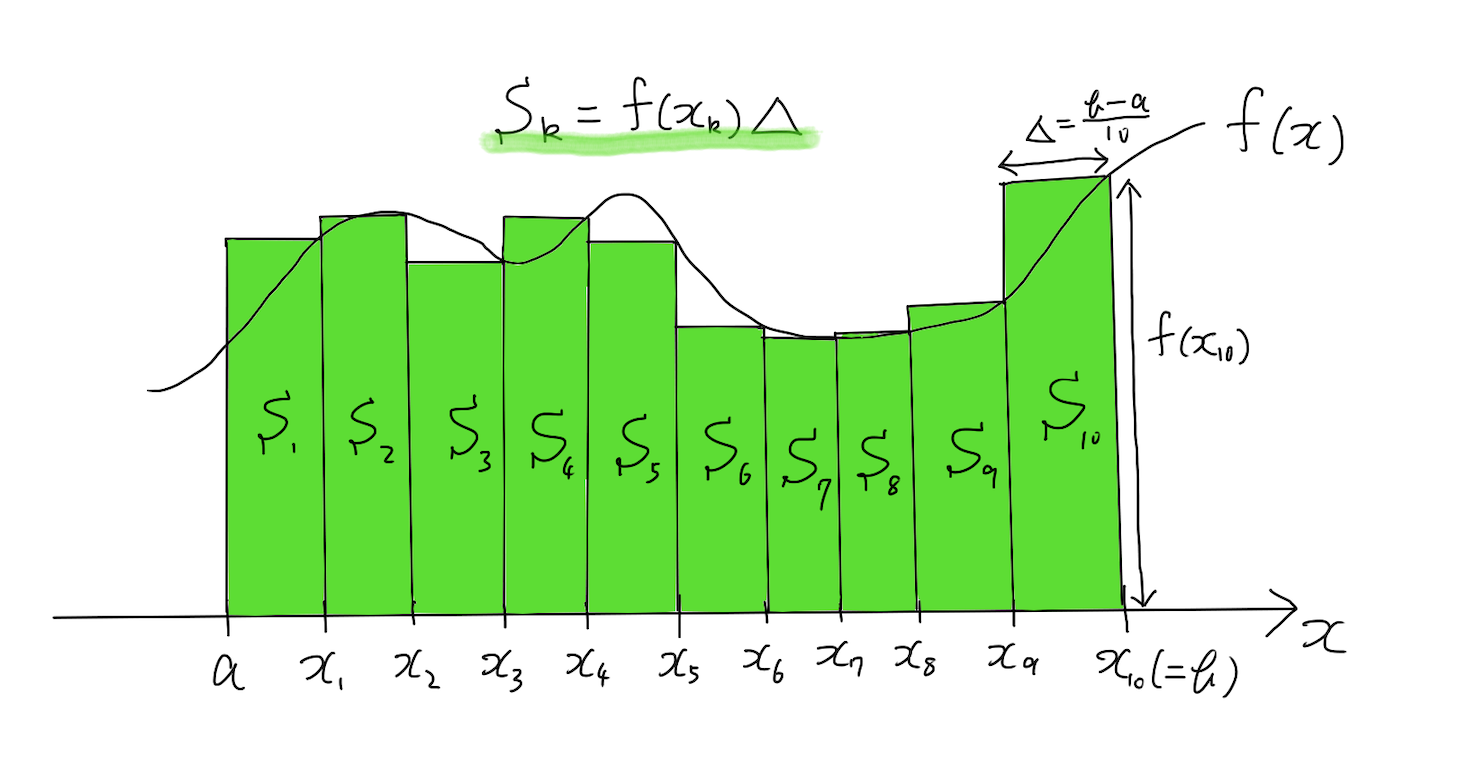
試してみよう
ここでは \(f(x)=\sqrt{x}\) として、(式1)の右辺の和を計算してみましょう。
積分する範囲( \(a\) から \(b\) )と、分割する数 \(n\) を入力し、「計算」を押してください。
\(n=10,20,…\) と大きくしていくと、和が解析解に近づく様子をみてみましょう。
\( a = \)
\( b = \)
\( n = \)
\( b = \)
\( n = \)
※ \(a\) は \(0\) 以上の値、 \(n\) は50以下の自然数を設定してください
———- 表示ここから ———-
解析解
(式1)の右辺の和
———- 表示ここまで ———-

