掛け算の筆算を図形で考える

概要

掛け算の筆算でやっていることを、図形で考えてみます。

２桁同士の掛け算の例

具体例として、\(21 \times 32\) を考えます。

筆算

\begin{eqnarray}
\Large{
\begin{array}{rr}
& 21 \\
\times) & 32 \\ \hline
& 42 \\
& 63 \hspace{0.65em} \\ \hline
& 672
\end{array}
}
\end{eqnarray}

これは、次のように計算しているのと同じです。

長方形の面積で考える

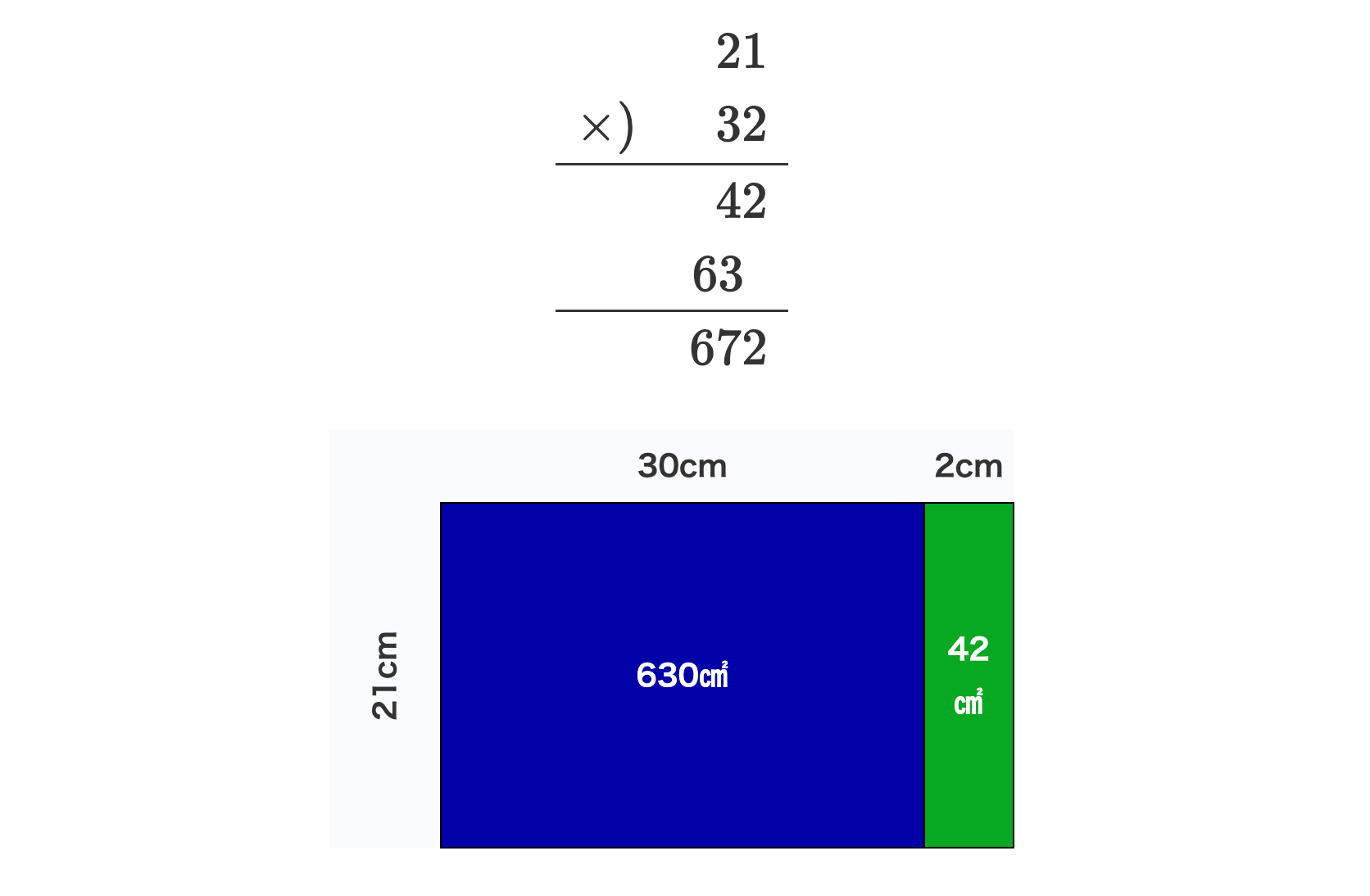
上記の例は、縦21cm\(\times\)横32cm の長方形の面積を求める問題に置き換えられます。

横の長さを30cmと2cmに分割し、それぞれの面積を足せば全体の面積が求まります。

好きな数値で試そう

好きな自然数を2つ選んで、筆算を長方形の面積と比べてみましょう。
自然数 \(a,b\) を入力し、計算ボタンを押してください。

• 自然数は1〜99の範囲で入力してください

———- 表示ここから ———-

———- 表示ここまで ———-

あとがき

今回は２桁同士の掛け算を考えましたが、３桁以上になっても考え方は同じです。