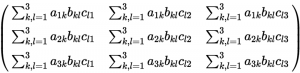概要
行列表示は次元が大きくなると書くのがしんどい。
例えば3×3の行列\( A,B,C \)の積などあまり考えたくない。
このような場合は、行列 \(A \)の \(ij\) 成分を\( a_{ij} \)と表記してシグマ記号を使うとシンプルになり、
紙面の節約にもなって環境にもやさしい。
具体的に、3×3の行列の積 \( S = ABC \) の \(ij\) 成分 \( s_{ij} \) は次のように表記できる。
例えば3×3の行列\( A,B,C \)の積などあまり考えたくない。
このような場合は、行列 \(A \)の \(ij\) 成分を\( a_{ij} \)と表記してシグマ記号を使うとシンプルになり、
紙面の節約にもなって環境にもやさしい。
具体的に、3×3の行列の積 \( S = ABC \) の \(ij\) 成分 \( s_{ij} \) は次のように表記できる。
\begin{align}
s_{ij} = \sum_{k,l}^3 a_{ik}b_{kl}c_{lj}
\end{align}
s_{ij} = \sum_{k,l}^3 a_{ik}b_{kl}c_{lj}
\end{align}
行列表示での確認
行列の次元\(n\)に対して3つの行列の積の成分が上記の式のようになっているか、
行列形式での展開の過程を確認します。
次元 \( n = \) (最大5)
行列形式での展開の過程を確認します。
次元 \( n = \) (最大5)
———- 表示ここから ———-
———- 表示ここまで ———-
あとがき
最近は行列計算のライブラリが充実しているので、
学生のレポートでもない限り手計算はしないほうがいいだろう。
ただ、具体的な計算ではなく概念の説明となると式が必要になる。
シグマ記号という表現方法がなかったら発狂すると思う。