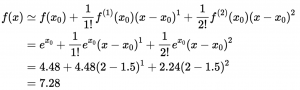概要
物理学で近似解を求めるためにテイラー展開をよく使っていましたが、
実際のところ近似できているのかよくわかっていませんでした。
EMANさんのページを読むと、対象とする関数の収束半径によっては
注意する必要があるような気がします。
EMANの物理学・物理数学・テイラー展開
ということで、収束半径が無限大の場合とそうでない場合で、
好きな点のまわりでテイラー展開したらどうなるか調べてみます。
対象とする関数
収束半径が無限大の関数の例として \( f(x) = e^x \) を、
収束半径が\(1\)の関数の例として、\( g(x) = log(1+x) \) を考えます。
それぞれの関数を、\( x = x_0 \) まわりでテイラー展開してみましょう。
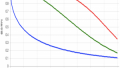
\( x – x_0 \) が小さいほど、また\(n\)が大きいほど実際の値に近づくことを確認しましょう。
また、\( g(x) \) については \( x – x_0 \) と収束半径の関係に注目しながら確認しましょう。
収束半径が\(1\)の関数の例として、\( g(x) = log(1+x) \) を考えます。
それぞれの関数を、\( x = x_0 \) まわりでテイラー展開してみましょう。
\( x – x_0 \) が小さいほど、また\(n\)が大きいほど実際の値に近づくことを確認しましょう。
また、\( g(x) \) については \( x – x_0 \) と収束半径の関係に注目しながら確認しましょう。
\( x = \)
\( x_0 = \)
展開する項数(最大20)\( n = \)
\( x_0 = \)
展開する項数(最大20)\( n = \)
\( x=x_0 \) まわりでのテイラー展開の結果
———- 結果表示ここから ———-
———- 結果表示ここまで ———-
考察
\( x = 2.0, x_0 = 0.0 \)とすると、\( f(x) = e^x \) は\(n\)を大きくすれば近似できますが、
収束半径が\(1\)である\( g(x) = \log(1+x) \)は大変なことになります。
ただ、\( x-x_0 \)が十分小さいことを仮定できれば、
テイラー展開の第2項くらいまでで近似しても大丈夫そうです。