地球の陸地を平面地図に投影したときの拡大率を求める

概要

地球儀は球面に分布する陸地を正しい縮尺で示しますが、平面の地図に示すと歪みが生じます。赤道を基準とした地図では緯度が高くなるほど（極に近づくほど）、実際より大きく投影されます。

イメージ

この現象がよく理解できるページ（The True Size Of …）を見つけました。
同ページで日本を高緯度にずらした様子を、動画で示します。

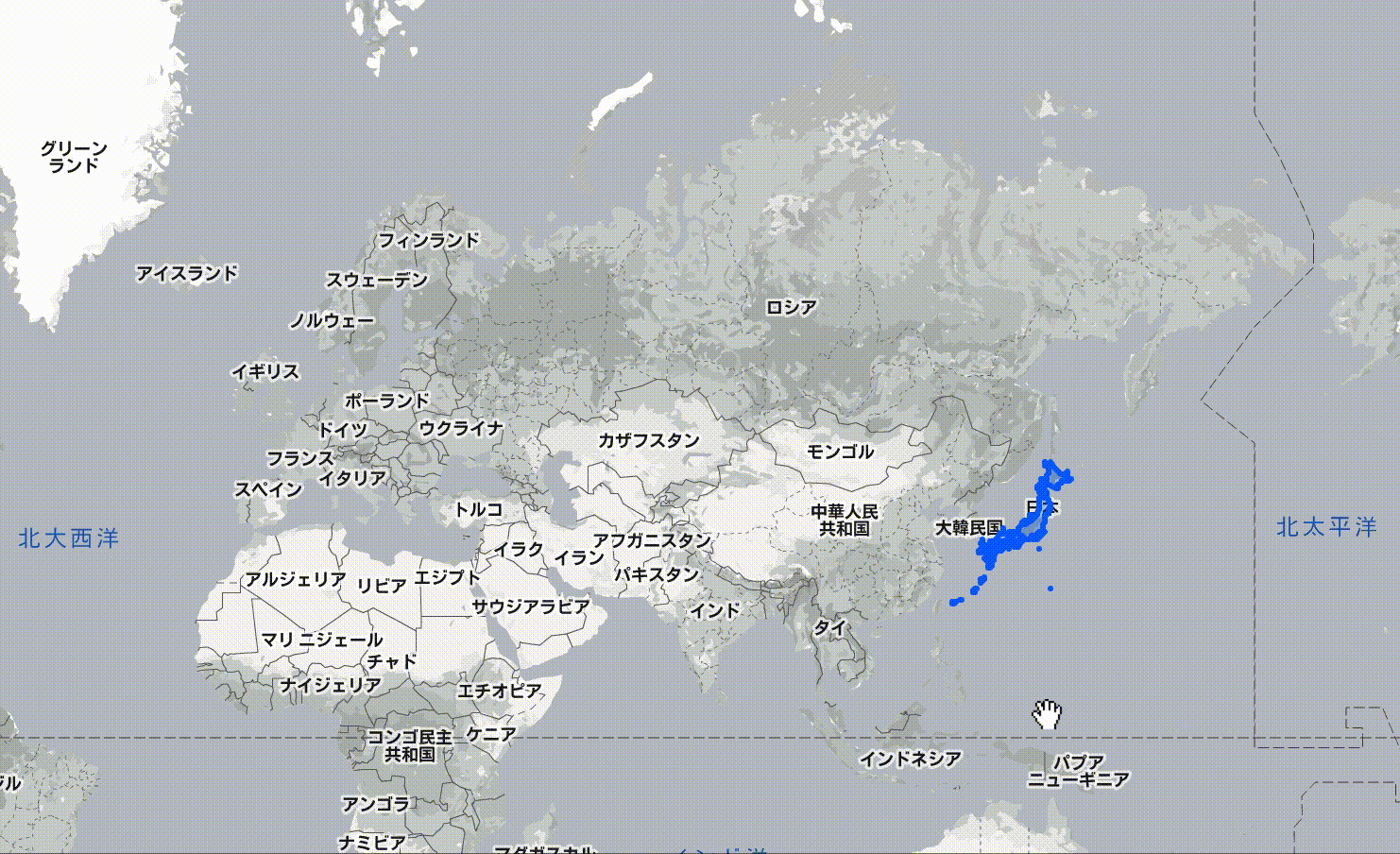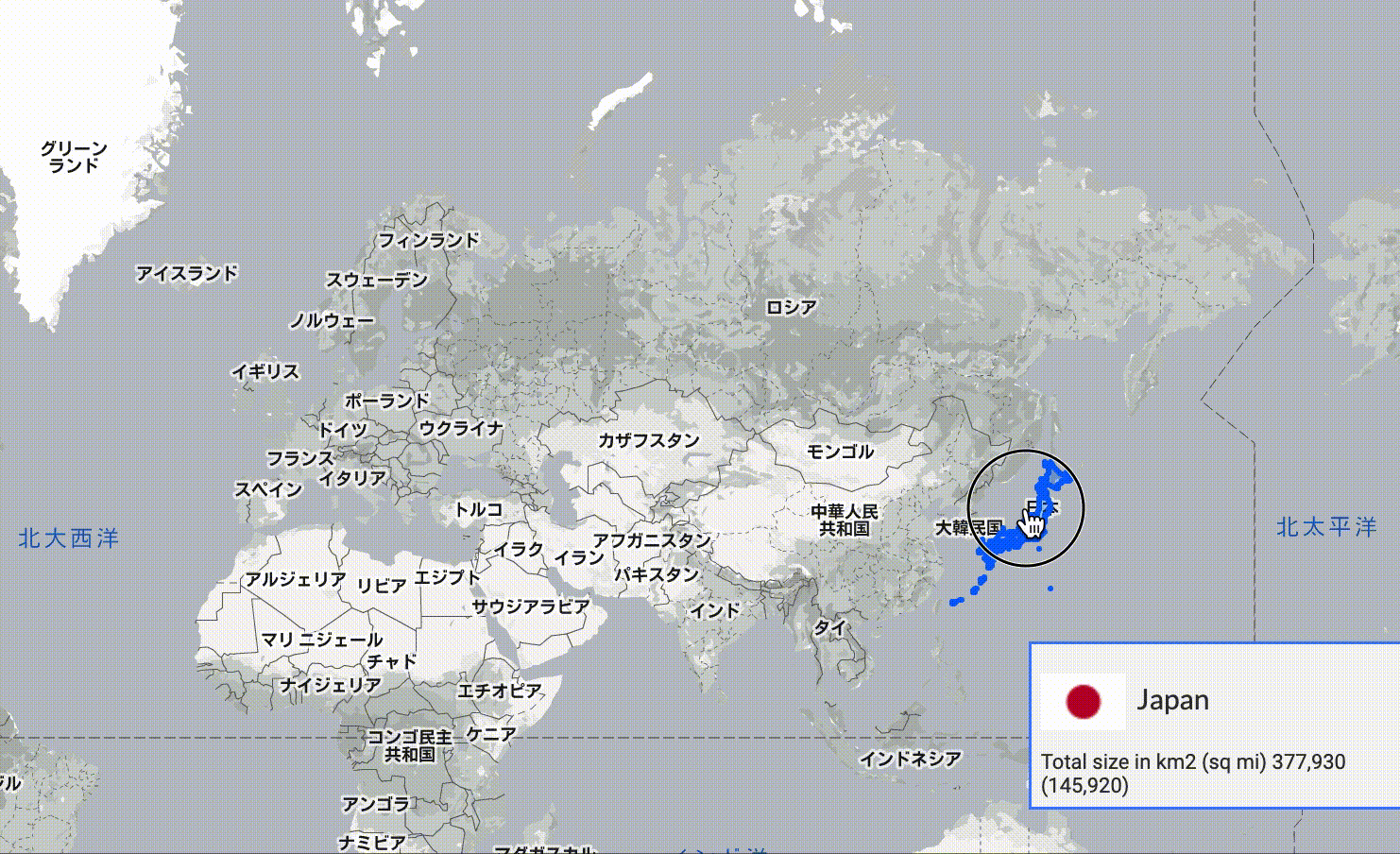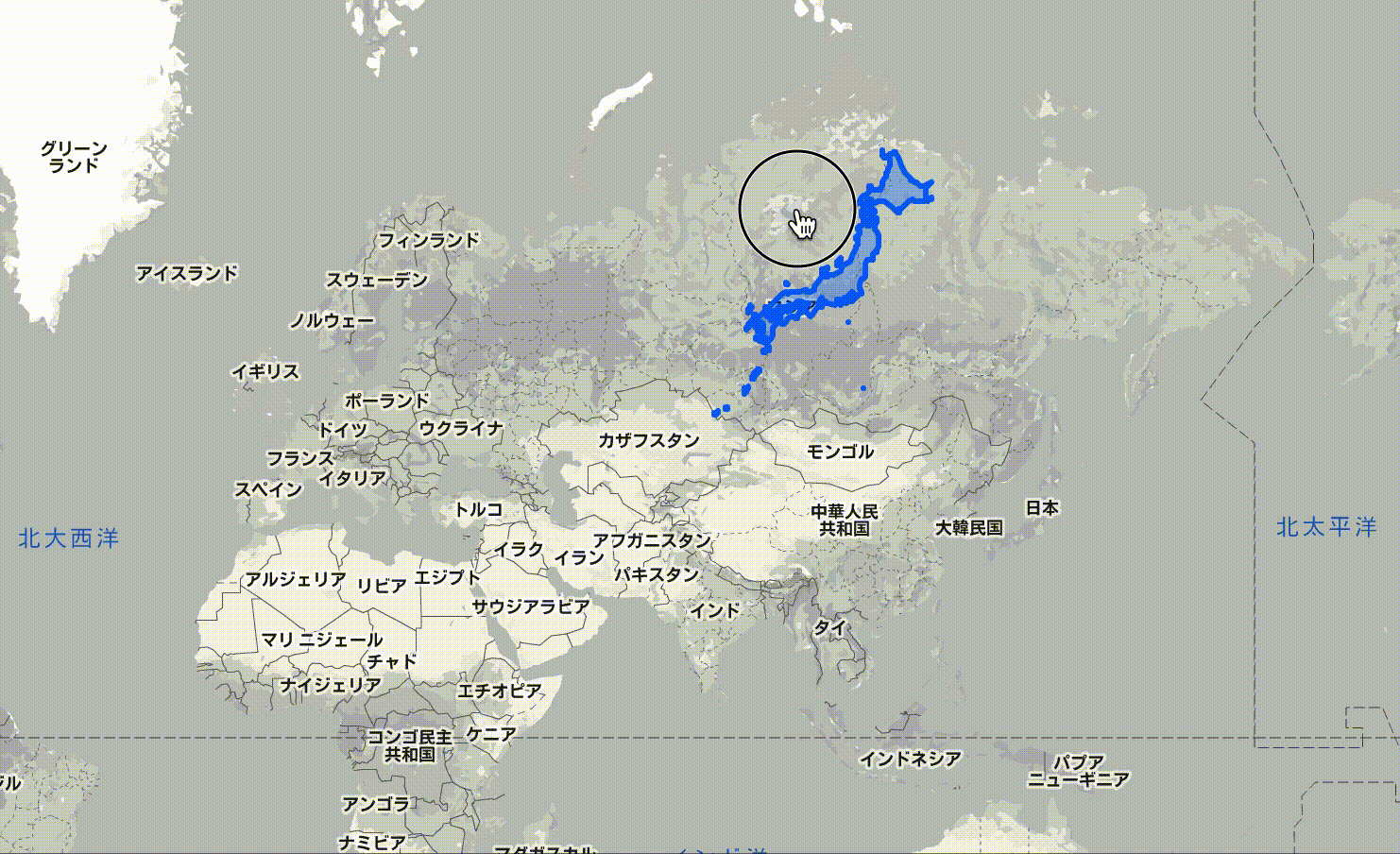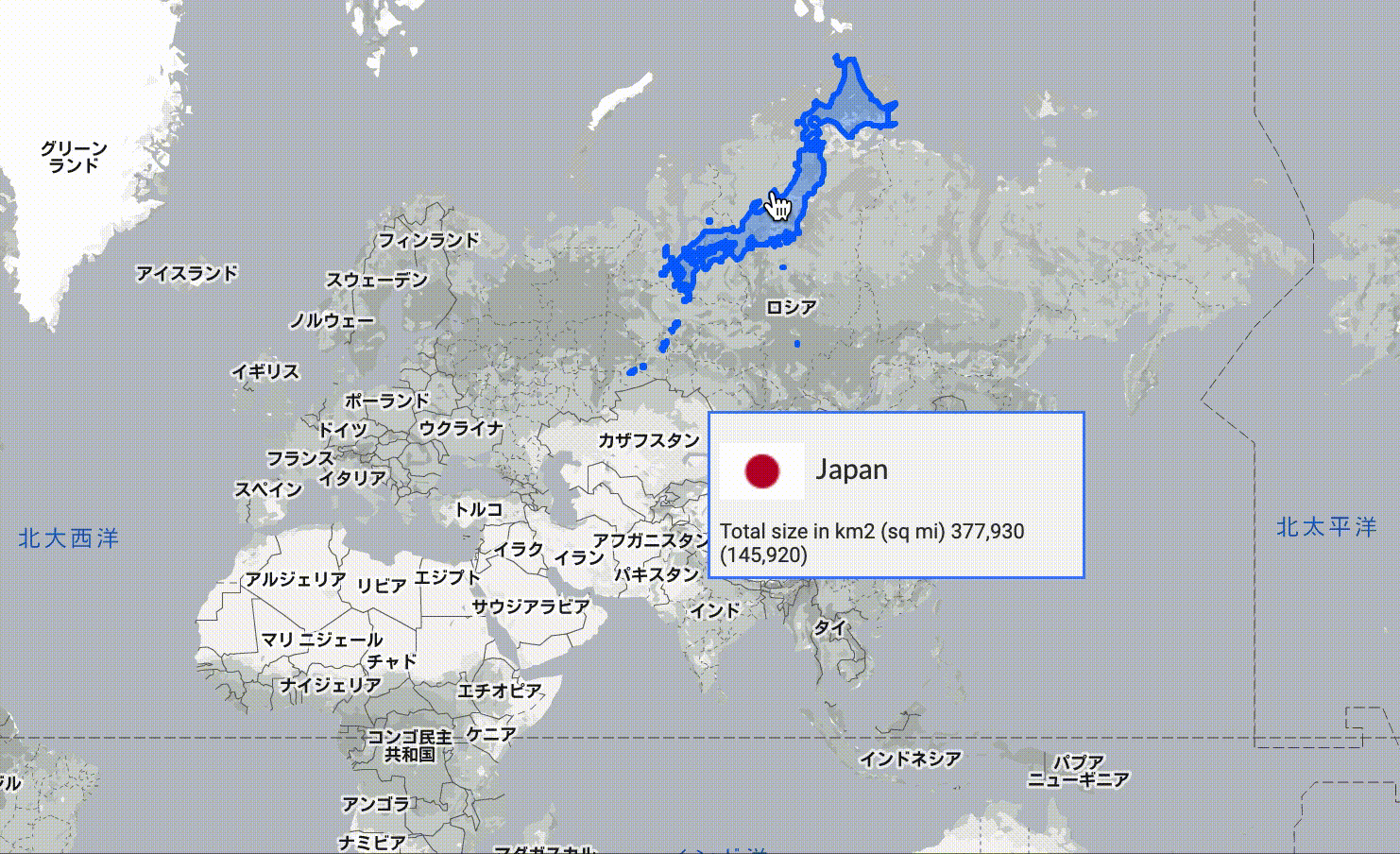
高緯度では、日本が縦横ともに大きく示されることがわかります。
例えばロシアは高緯度に位置するため、赤道付近の国々と比べると大きく引き伸ばされていると考えられます。

本記事で考える平面への投射方法

本記事では、地球を円筒で囲み、地球の中心から見て球面を円筒に投影し、その円筒を展開する方法（正軸円筒図法）を考えます。

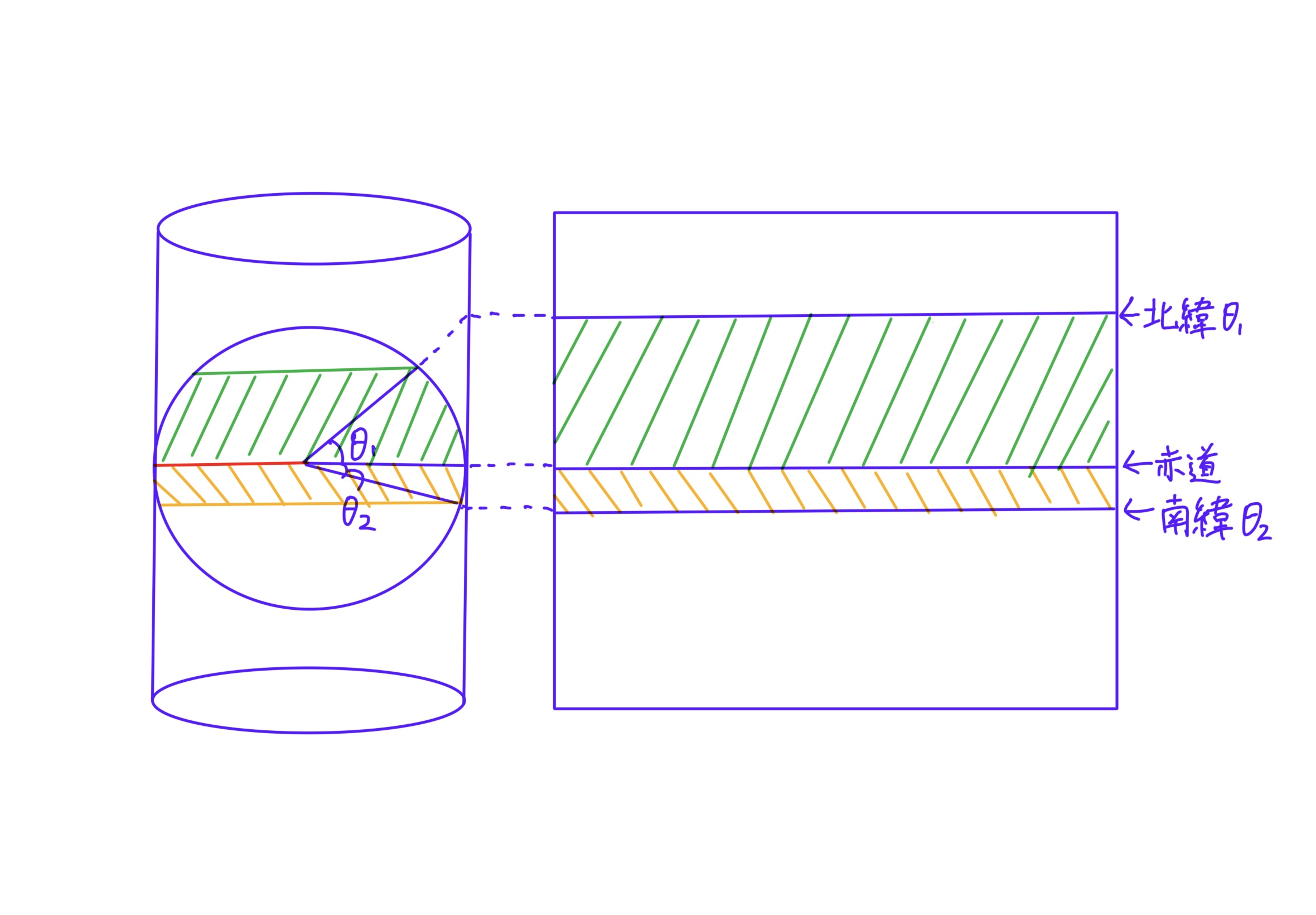
正軸円筒図法のイメージ

円筒に接する赤道は等倍ですが、緯度が高くなるほど平面図では東西および南北方向に引き延ばされます。

東西方向の拡大率

まず、緯度 \(\theta\) における東西方向の拡大率について見てみます。

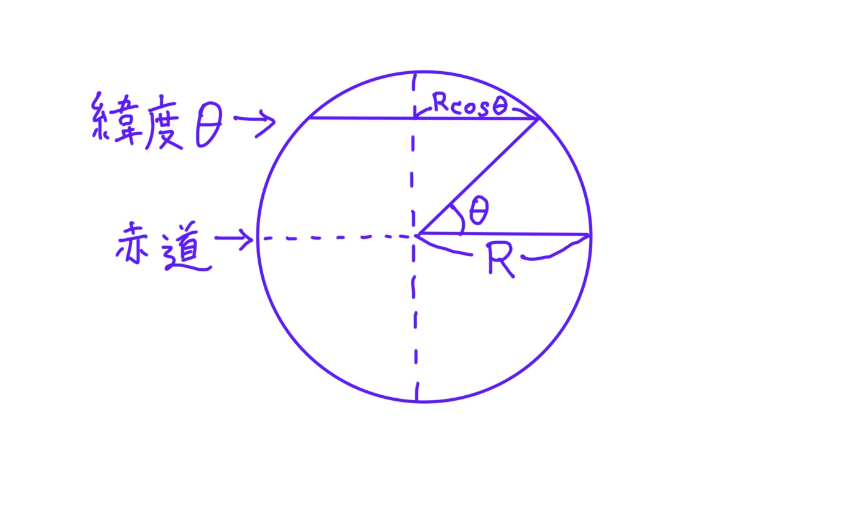
地球の半径を \(R\) とすると、緯度 \(\theta\) の緯線が囲む円の半径は \(R\cos\theta\) です。よって、緯度 \(\theta\) の緯線の周長は、赤道の周長の \(\cos\theta\) 倍です。

平面図では緯線の両端が赤道と同じ長さに揃えられるため、緯度 \(\theta\) 上の陸地は東西方向に \(1/\cos\theta\) 倍引き延ばされます。

例えば、ロシアの西部にある首都モスクワの緯度は、\(55.7558\)度です。\(\cos55.7558^\circ = 0.563\) なので(※1)、この緯線上にあるロシア領土は、平面地図では東西方向に \(1/0.563 = 1.78\) 倍引き延ばされます。
(※1)ke!sanというサイトで計算できます。

南北方向の拡大率

次に、緯度 \(\theta\) 付近での南北方向の拡大率について見てみます。

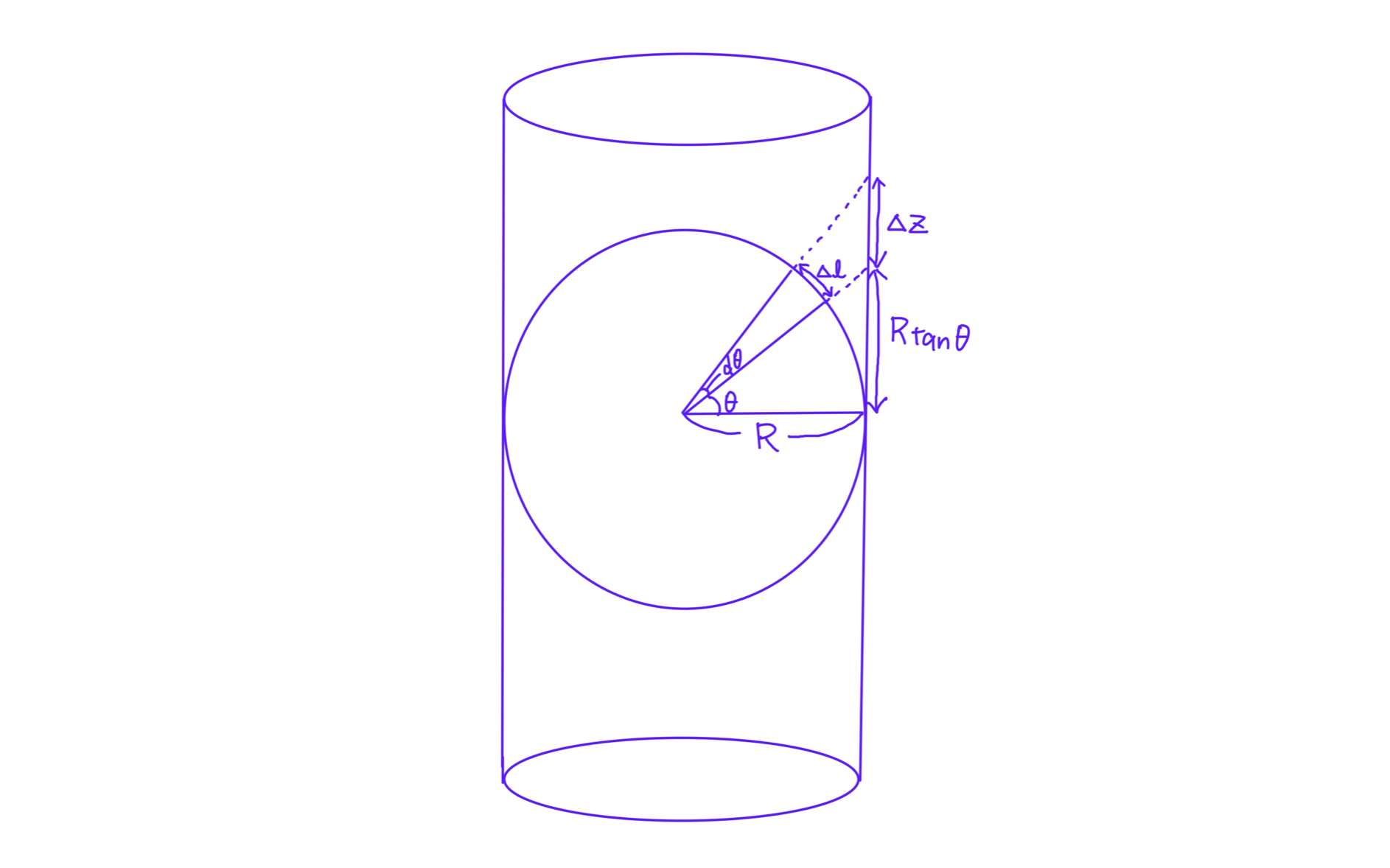
球面での南北方向の区間 \(\Delta l\) は、円筒に投影すると上図の \(\Delta z\) に引き延ばされます。緯度 \(\theta\) が大きいほど、引き延ばされる比率 \(\Delta z/\Delta l\) も大きくなります。

\(\Delta l = R\Delta \theta\) なので、
\begin{eqnarray}
\frac{\Delta z}{\Delta l} = \frac{R\tan(\theta + \Delta \theta) – R\tan\theta}{R\Delta\theta} = \frac{\tan(\theta + \Delta \theta) – \tan\theta}{\Delta\theta}
\end{eqnarray}

例によって、モスクワ周辺での南北方向の拡大率を考えます。緯度が55度から56度までの南北方向の区間（緯度１度差）にて、球面での距離 \(\Delta l\) に対する円筒に投影される距離 \(\Delta z\) の比率を求めます。

\begin{eqnarray}
\frac{\Delta z}{\Delta l} = \frac{\tan(55^\circ + 1^\circ) – \tan55^\circ}{\pi/180} = \frac{1.483 – 1.428}{0.0175} = 3.14
\end{eqnarray}
(※)\(\Delta \theta = 1^\circ = \pi/180 [rad]\)

モスクワ周辺の緯度では、１度分の距離が3.14倍に引き延ばされて平面地図に投影されることになります。高緯度にいけば、さらに引き延ばされます。