三角関数(sin,cos)を任意の区間で積分する

三角関数（sin,cos）の積分をする時、様々な性質を利用することが多いです。
ここでは、基本的な形の三角関数 $\sin(mx), \cos(mx)$ を任意の区間で積分し、その特徴を見ることにします。

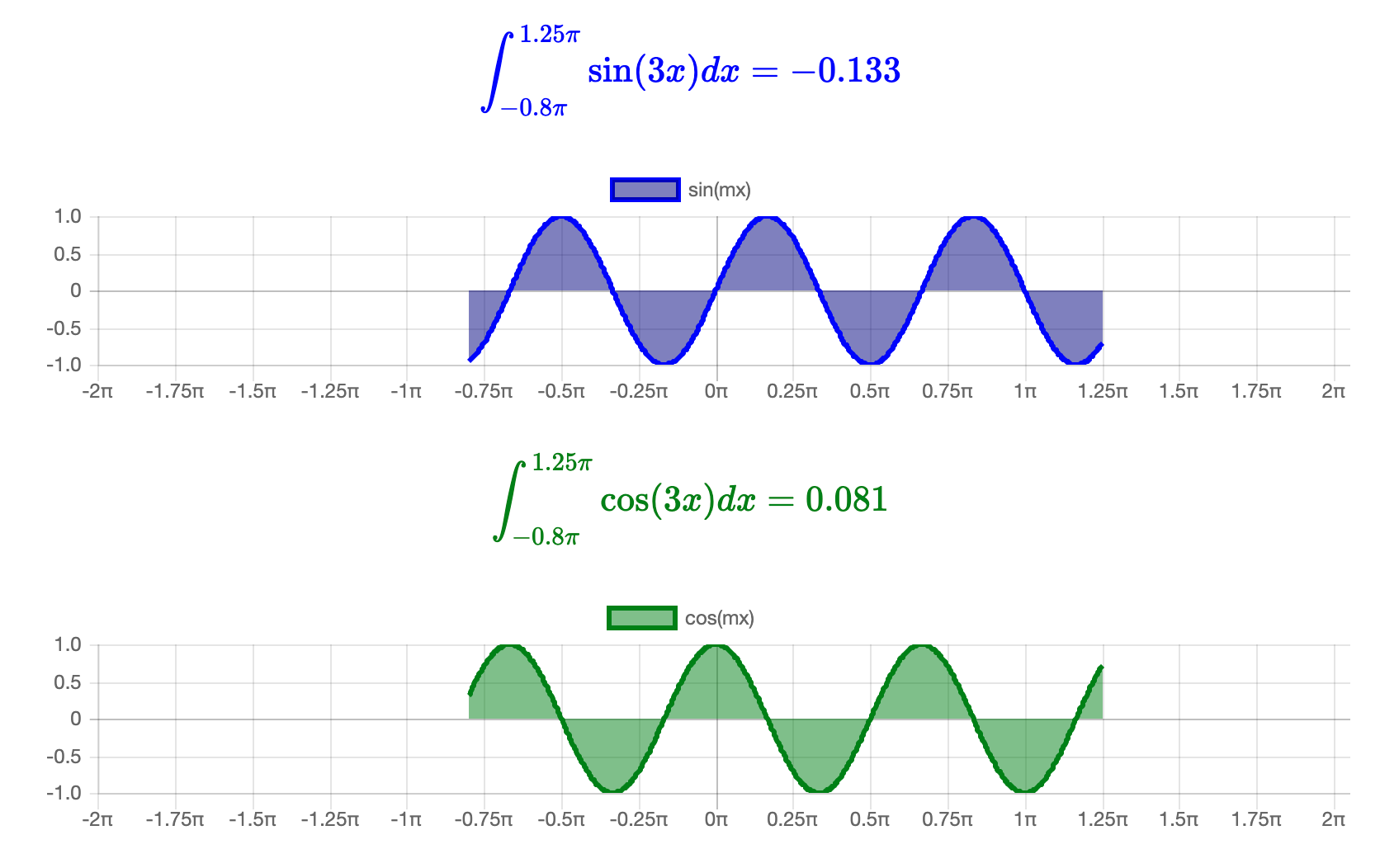
次の2種類の積分を考えます。
$\begin{eqnarray} \int_a^b \sin(mx)dx \\ \int_a^b \cos(mx)dx \end{eqnarray}$

まず、三角関数の対称性による基本的な特徴を見てみましょう。
$m=1$ のとき、 $\sin(x),\cos(x)$ の周期 $2\pi$ で積分すると、プラス部分とマイナス部分が打ち消しあって $0$ になることがわかります。

$\begin{eqnarray} \int_{-\pi}^{\pi} \sin(x)dx = 0 \end{eqnarray}$

$\begin{eqnarray} \int_{-\pi}^{\pi} \cos(x)dx = 0 \end{eqnarray}$

区間 $[a,b]$ と $m$ を色々と変えて積分してみましょう。
整数でなくても大丈夫です。

下記の条件を満たす $a,b,m$ を入力し、「表示」ボタンを押してください。
$a,b$ は、それぞれ [入力値 × $\pi$ ] となります。

$a=$

$\pi$

$b=$

$\pi$

$m=$

———- 表示ここから ———-

———- 表示ここまで ———-

色々と試して見ると、例えば次の特徴が確認できます。

今回は $\sin(mx)$ と $\cos(mx)$ を別々に積分しましたが、積 $\sin(mx) \cos(nx)$ を積分すると別の特徴も見えてきます。次の記事で紹介しているので、ご参照ください。