ユークリッドの互除法で最大公約数を求める

概要

ある2つの自然数の最大公約数を求める方法として、ユークリッドの互除法が知られています。ここでは、図形を利用して互除法の考え方を見てみます。

ユークリッドの互除法とは

Webで調べると色々出てくるので説明しませんが、下記の動画がすごくわかりやすいです。動画は4分弱です。

図形を利用した互除法の考え方

まず、上記の動画で紹介されていた例と同じく、\(221\) と \(153\) の最大公約数をユークリッドの互除法で求めてみます。

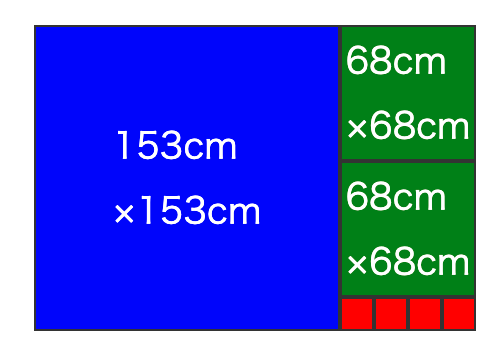
上記の式は、\(221cm × 153cm\) の長方形の長辺を短辺で割ったときの、商と余りを示していることがわかります。

これより、\(221cm × 153cm\) の長方形は、次のように３種類の正方形で分割できることがわかります。

長辺も短辺も \(17\) で割切れるので、\(221\) と \(153\) の最大公約数は \(17\) です。

パラメータ設定

好きな自然数を2つ選んで、最大公約数を求めてみましょう。
自然数 \(a,b\) を入力し、計算ボタンを押してください。

• 自然数は1〜9999の範囲で入力してください
• \(a,b\) と最大公約数の差が大きい場合、図形が崩れることがあります

計算

———- 表示ここから ———-

———- 表示ここまで ———-

あとがき

数式で記述するには代数が便利ですが、視覚的に理解するときは幾何学が威力を発揮しますね。