十進数からn進数への変換

概要

十進法から二進法に変換する方法はよく知られており、Webで検索すると色々なサイトに載っています。

ここでは、この変換方法の解釈を考えたいと思います。

とりあえず変換してみる

例として、73を十進数から二進数に変換してみます。

素因数分解の要領で分解していき、余りを下から順に並べると二進数での表記\((1001001)_2\)が得られます。

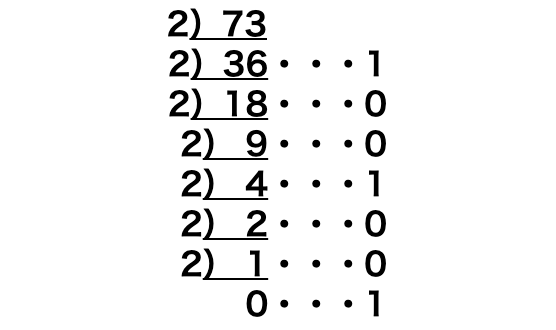
これは、次のように展開しているのと同じです。

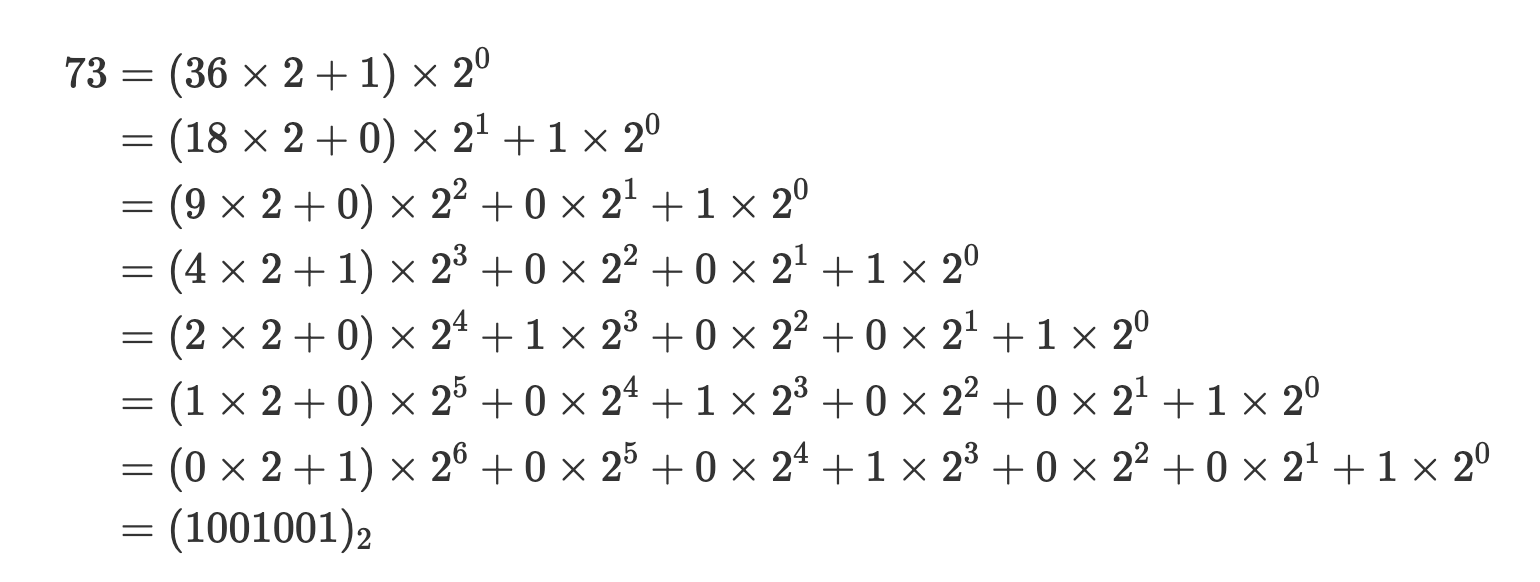
最終行の結果を見ると、73には\(2^6\)が1つ含まれることが分かります。一方で、筆算に現れる過程を縦方向に見ると、73には「2で6回割り切れる成分が1つ含まれる」と捉えることもできます。同様に、\(1\times2^3\)の項は「2で3回までなら割り切れる成分が１つ含まれる」ことを意味しています。